|
|
Stage One: Light Reflection Models
Cornell University Program of Computer Graphics |
|
||||
|
Note: This page describes stage one of a research framework for global illumination which was first presented at a special SIGGRAPH session in August of 1997. The full text of the paper is available from the Program of Computer Graphics on-line publications.
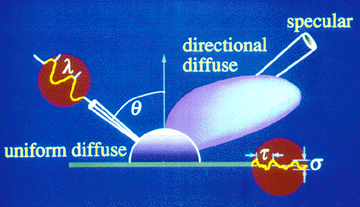
Components of a light reflection model, showing incoming light and outgoing diffuse, directional diffuse, and specular reflections
ModelsLight reflectance models have always been of great interest to the computer graphics community. The most commonly used model was derived approximately twenty-five years ago at the University of Utah [PHON75]. The Phong direct lighting model is a clever scheme using a simple representation, but it is neither accurate in the sense that it represents the true reflection behavior of surfaces, nor its it entry consistent.Despite notable improvements in the Phong model over the years [BLIN77][COOK81], a comprehensive model of how light reflects or transmits when it hits a surface, including its subsurface interactions, needs to be developed. The resulting bidirectional reflectance distribution function (BRDF) is a function of the wavelength, surface roughness properties, and the incoming and outgoing directions. The BRDF should correctly predict the diffuse, directional diffuse, and specular components of the reflected light. In 1991, He [HE91] presented a sophisticated model based on physical optics and incorporating the specular, directional diffuse, and uniform diffuse reflections by a surface. Related work [POUL90][OREN94] also provides models applicable to a wide range of materials and surface finishes, but for more complex surfaces, such as layered surfaces or thin films, analytical derivations are often too complicated. In some cases, Monte Carlo methods have been applied for simulating local reflectance properties on a micro scale [KAJI85][CABR87][HANR93].
RepresentationsUltimately, what is necessary is a compact representational scheme which can accurately describe the dominant behavior of a BRDF. The representation method should be suitable for progressive algorithms, monotonically converging to a correct solution. This past year, we introduced a new class of primitive functions with nonlinear parameters for representing reflectance functions. The functions are reciprocal, energy-conserving, and expressive, and capture important phenomena such as off-specular reflection, increasing reflectance with angle of incidence, and retroreflection [LAFO97]. Most importantly, the representation is simple, compact, and uniform and has been verified by comparisons to our physically-based model and actual measurements.

The sphere on the left uses a diffuse reflection representation, while the one on the right and the metal panel illustrate rendering with a more sophisticated representation [LAFO97]
MeasurementFor verification of our light reflection models we rely on physical measurement of light sources, surface reflections from physical samples of materials, and the input geometry for our test scenes.Though significant progress has been made in modeling the surface BRDF, the model is far from complete. Properties such as polarization and anisotropy need to be well accounted for. Subsurface scattering which contributes towards the diffuse component of the BRDF is not well understood and is being handled empirically. Surface properties other than the BRDF which affect light interaction such as transmission, fluorenscence, and phosphorescence are either completeley ignored or are being modeled empirically. These need to be correctly accounted for. The most accurate available scene geometry, light source emission data and surface reflection functions (BRDF's) serve as input data for simulating the light transport in stage two of our research framework. GoalsIn summary, our specific long-term goals for light reflection models are:
Lead Researchers and Collaborators
Publications
References
| ||||||
| ||||||